Il y a plein de choses que j’aurais aimé connaître à 18 ans et les intérêts composés est le sujet numéro 1 dans cette liste.
Ça m’aurait certainement permis de devenir riche à l’heure actuelle, ou du moins avoir un revenu complémentaire très confortable.
Albert Einstein aurait dit que « L’intérêt composé est la huitième merveille du monde. Celui qui peut bien comprendre l’intérêt composé en bénéficie, celui qui ne le comprend pas le paie ».
En d’autres termes, il faut maîtriser la puissance des intérêts composés pour devenir riche.
Les intérêts composés, qu’est-ce que c’est ?
Un intérêt est le revenu régulier payé par un investissement à son détenteur. Par exemple, les dividendes d’une action ou d’un ETF, les coupons d’une obligation ou les loyers d’une SCPI ou d’un bien immobilier sont les intérêts de ces placements.
À ce stade, il s’agit d’intérêts simples qui peuvent être consommés au moment de leur paiement comme complément de revenu, rente ou encore pension de retraite.
Si au lieu d’être consommés ils sont réinvestis dans le placement (par exemple en rachetant plus d’actions ou de SCPI), ils deviennent des intérêts composés. Ils sont dits composés car dorénavant ils vont eux-mêmes générer des intérêts.
Voici un exemple pour illustrer la différence entre les intérêts simples et composés :
Considérons un placement de 100 euros qui rapporte 10% par an. La première année ce placement rapporte 10 euros.
Intérêt simple : ces 10 euros sont consommés. Du coup la deuxième année, il n’y a que 100 euros investis et produisent encore 10 euros d’intérêt.
Intérêt composé : ces 10 euros sont réinvestis. Ainsi la deuxième année, il y a 110 euros investis qui produisent 11 euros d’intérêt.
Les intérêts composés ont produit 1 euro de plus la deuxième année. Cet effet se décuple au cours du temps et finit par produire un effet boule de neige au bout de quelques années.
Là où l’intérêt simple continuera à produire 10 euros par an, l’intérêt composé produira plus de 20 euros par an au bout de 8 ans.
Ainsi au bout de 8 ans le revenu annuel est doublé et se phénomène s’accentue avec le temps.
C’est ainsi que les intérêts composés permettent d’avoir un revenu complémentaire voire d’atteindre l’indépendance financière.
Comment calculer les intérêts composés ?
Considérons une somme S placée à un taux d’intérêt annuel i.
Cette somme devient S x (1+i) au bout de 1 an.
Au bout de 2 ans cette somme devient : S x (1+i)²
Au bout de n années cette somme devient :
Là il s’agit de la formule mathématique qui vous donne le résultat de l’investissement : c’est la formule des intérêts composés.
Cependant, les calculs deviennent fastidieux si vous avez un placement initial et des versements réguliers.
C’est pour cette raison que j’ai créé une calculatrice d’intérêts composés qui ne vous donne pas seulement la valeur de votre capital futur mais en plus le montant de vos gains ainsi que votre revenu mensuel au terme de votre investissement :
Devenir riche avec 10000 euros
Les intérêts composés sont réellement magiques et même si je sais comment les calculer depuis longtemps, je n’ai malheureusement réalisé leur puissance que très tard.
Je voudrais ici que vous preniez vraiment le temps de regarder cet exemple de calcul d’intérêts composés et que vous réalisiez l’impact que cet effet peut avoir sur votre épargne, vos investissements et votre liberté financière.
La bourse américaine a généré historiquement près de 10% par an de rendement sur le long terme.
Bien évidemment c’est le taux d’intérêt composé moyen et il y a eu des années avec un rendement supérieur et d’autres avec un rendement inférieur. C’est la volatilité des marchés.
Mais globalement le taux d’intérêt composé moyen de 10% par an est réaliste. Il peut par exemple être obtenu à travers un placement long-terme dans un ETF qui réplique le SP500.
Voici le résultat d’un investissement de 10 000 euros à 10% :
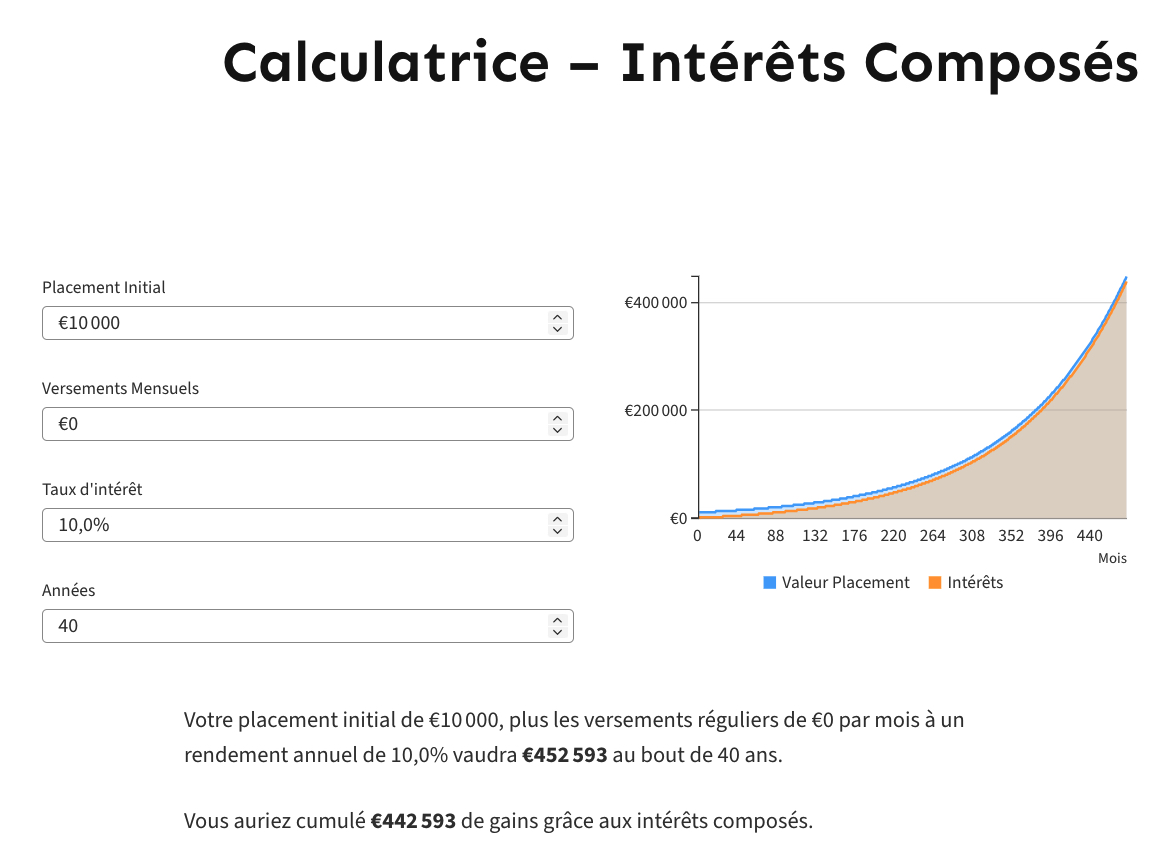
Ainsi au bout de 40 ans les 10 000 euros initiaux ont été multipliés par plus de 45 pour dépasser les 450 000 euros. En plus à partir de là ils génèrent plus de 45 000 euros par an en intérêts.
J’ai pris la durée de 40 ans car elle correspond à peu près à la durée d’une carrière professionnelle.
Cet exemple montre comment on peut avoir un capital supplémentaire de 450 000 euros à la retraite ou près de 45 000 euros de revenu complémentaire.
Il faut bien se rendre compte que la seule épargne ici a été de 10 000 euros au début et puis plus aucune épargne, plus aucun effort.
Les 440 000 euros supplémentaires ont été générés par le seul effet des intérêts composés. Ils ont permis à cet investisseur de devenir riche !
Vous voulez vivre librement sans subir les volontés d'un patron ?
Testez vos connaissances sur la liberté financière et découvrez les secrets de la richesse.
Comment devenir millionnaire ? [avec 100 euros par mois]
Dans cette section nous allons utiliser la calculatrice d’intérêts composés que j’ai développée et qui est disponible gratuitement dans la section Outils de ce blog.
Nous allons voir comment un petit effort d’épargne mensuel peut vous rendre millionnaire à la retraite.
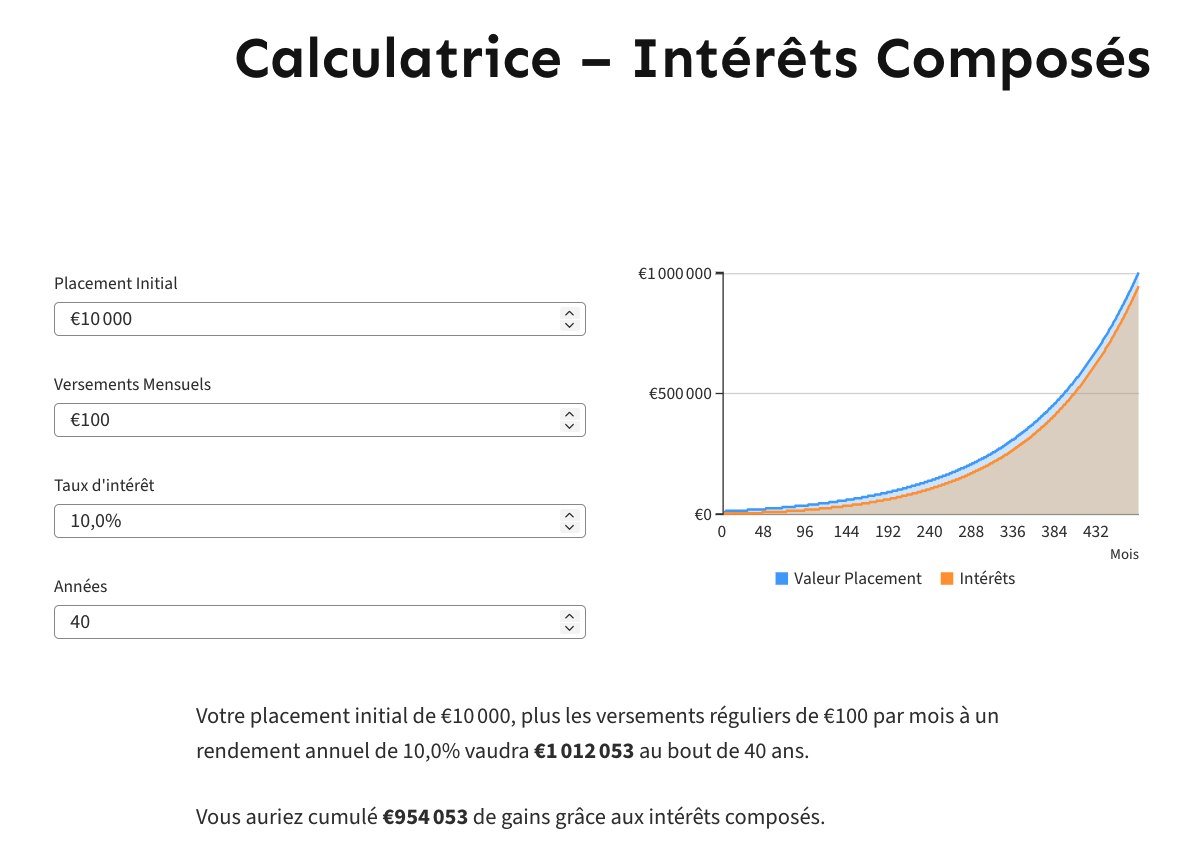
Supposons que vous suiviez l’investissement précédent et qu’en plus des 10 000 euros placés initialement vous ajoutiez 100 euros par mois. Les résultats sont édifiants :
Le capital cumulé à la retraite dépasse le million d’euros.
Il est exactement de 1 012 053 euros dont 954 053 euros sont des gains dus aux intérêts composés. Vous avez officiellement réussi à devenir millionnaire !
Les intérêts composés transforment chaque euro investi en plusieurs dizaines d’euros voire plusieurs centaines dans votre capital futur.
C’est pour cette raison que chaque euro épargné compte !
120 000 euros de plus pour moins de 5 euros par mois
J’ai aussi construit un simulateur d'épargne qui permet de faire des calculs plus avancés.
Il permet également d'analyser plusieurs scénarios possibles pour votre investissement.
Ce simulateur permet notamment de calculer l’impact d’une augmentation graduelle des versements mensuels que vous pouvez faire dans votre épargne.
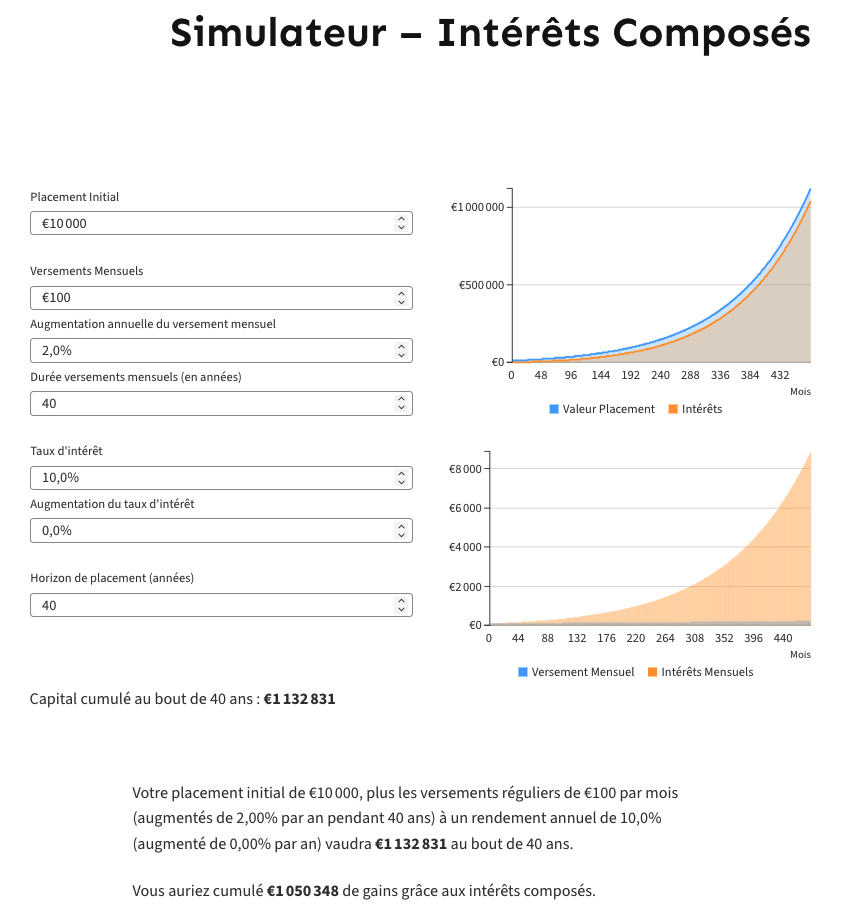
Reprenons l’exemple précédent et supposons que chaque année vous augmentiez votre versement mensuel de 2% car vous avez été augmenté ou vous avez reçu un bonus ou simplement vous voulez épargner plus.
Ainsi la deuxième année vous versez 102 euros mensuellement dans votre investissement et ça continue d’augmenter de 2% chaque année jusqu’au bout.
Cet effort d’épargne mensuel supplémentaire est indolore car il est de moins de 5 euros d’une année à l’autre.
Mais il permet de générer plus de 120 000 euros de capital additionnel à terme.
Le capital cumulé à la retraite atteint ainsi 1 132 831 euros dont 1 050 348 euros sont des gains grâce aux intérêts composés.
Une toute petite augmentation, d’immenses résultats
Imaginons que vous arrivez à améliorer le taux d’intérêt de votre placement de 0.5% parce que vous avez diminué vos frais ou parce que vous avez mieux diversifié vos placements. Vous obtenez ainsi 10.5% par an au lieu de 10%.
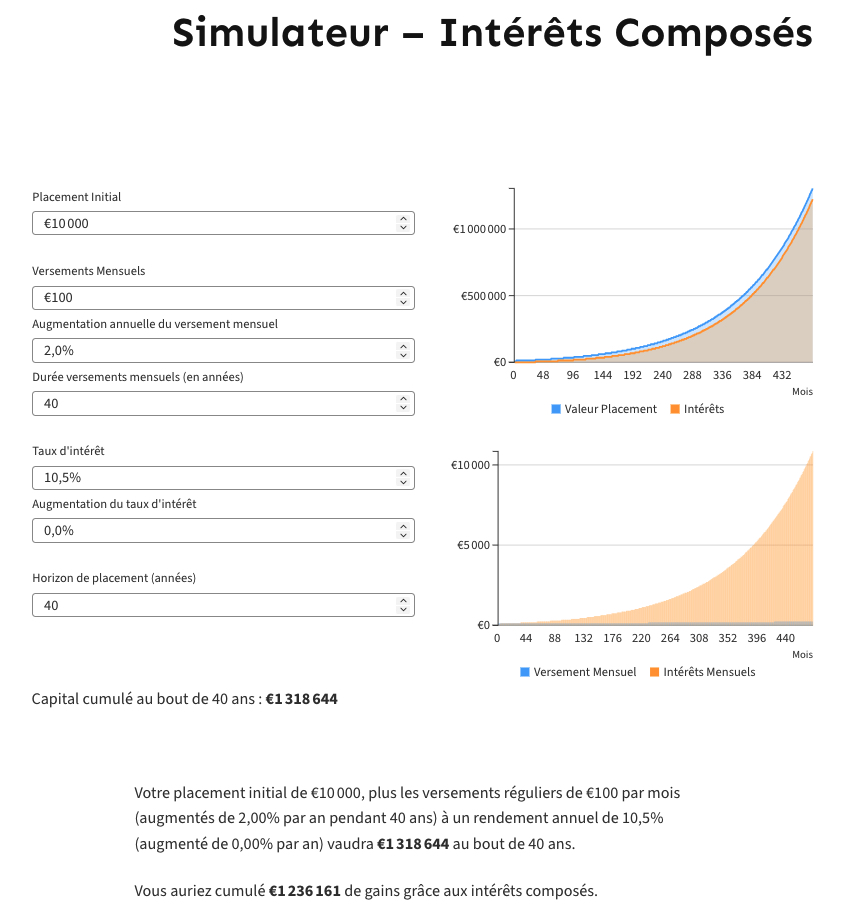
L’effet sur votre capital futur est considérable.
Votre épargne atteindra ainsi 1 318 644 euros à la retraite dont 1 236 161 euros sont des gains grâce aux intérêts cumulés.
En d’autres termes, une augmentation de 0.5% du taux d’intérêt a engendré près de 20% de capital en plus au terme du placement.
C’est la raison pour laquelle il faut faire attention aux frais qui grignotent de précieux pourcentages de la performance de vos investissements.
Transformer le temps en richesse grâce aux intérêts composés [sans effort]
Comme je l’explique dans mon article Combien peut-on gagner en bourse ? (par mois), je me suis intéressé au concept de liberté financière par ce que je voulais maîtriser mon temps et le consacrer à ce qui m’importe le plus.
Le temps est notre bien le plus précieux parce qu’il est irrécupérable.
Il se trouve que le temps est aussi la variable la plus importante en matière d’intérêts composés.
Pour illustrer ce fait, nous allons considérer deux scénarios : celui d’Anne et celui de Bertrand. Le simulateur d’intérêts composés permet de les analyser.
Anne : investir dès que possible
Anne a suivi le conseil de ses parents pour devenir indépendante financièrement. Elle avait épargné la majorité de l’argent qu’elle a reçu au fil des années pour ses anniversaires, noëls, ses réussites à l’école, au collège et au bac.
La jeune-fille avait aussi épargné une grosse part de l’argent qu’elle avait gagné de ses petits boulots d’été qu’elle avait eu l’habitude de faire depuis ses 14 ans.
Ainsi, elle s'est retrouvée à 18 ans avec une somme de 10 000 euros qu’elle a placée dans une assurance-vie avec des frais bas et investie en ETFs bien diversifiés qui rapportent en moyenne 10.5% par an.
Anne a également décidé d’y verser 50 euros par mois qu’elle avait économisé sur ses revenus de cours particuliers qu’elle avait donnés en parallèle de ses études de mathématiques.
Elle a continué à investir ses 50 euros par mois quand elle avait commencé à travailler.
Anne va fonder une famille 10 ans plus tard et arrêter de verser les 50 euros par mois dans son assurance-vie.
En effet, les frais de garde des enfants, le remboursement du prêt du pavillon en banlieue et des prêts de sa voiture et de celle de son compagnon ne lui permettaient plus de faire des économies.
Cependant elle gardera son capital investi jusqu’à sa retraite à l’âge de 62 ans, ce qui fait une durée totale d’investissement de 44 ans (de 18 ans à 62 ans).
Voici ce qu’elle obtient :
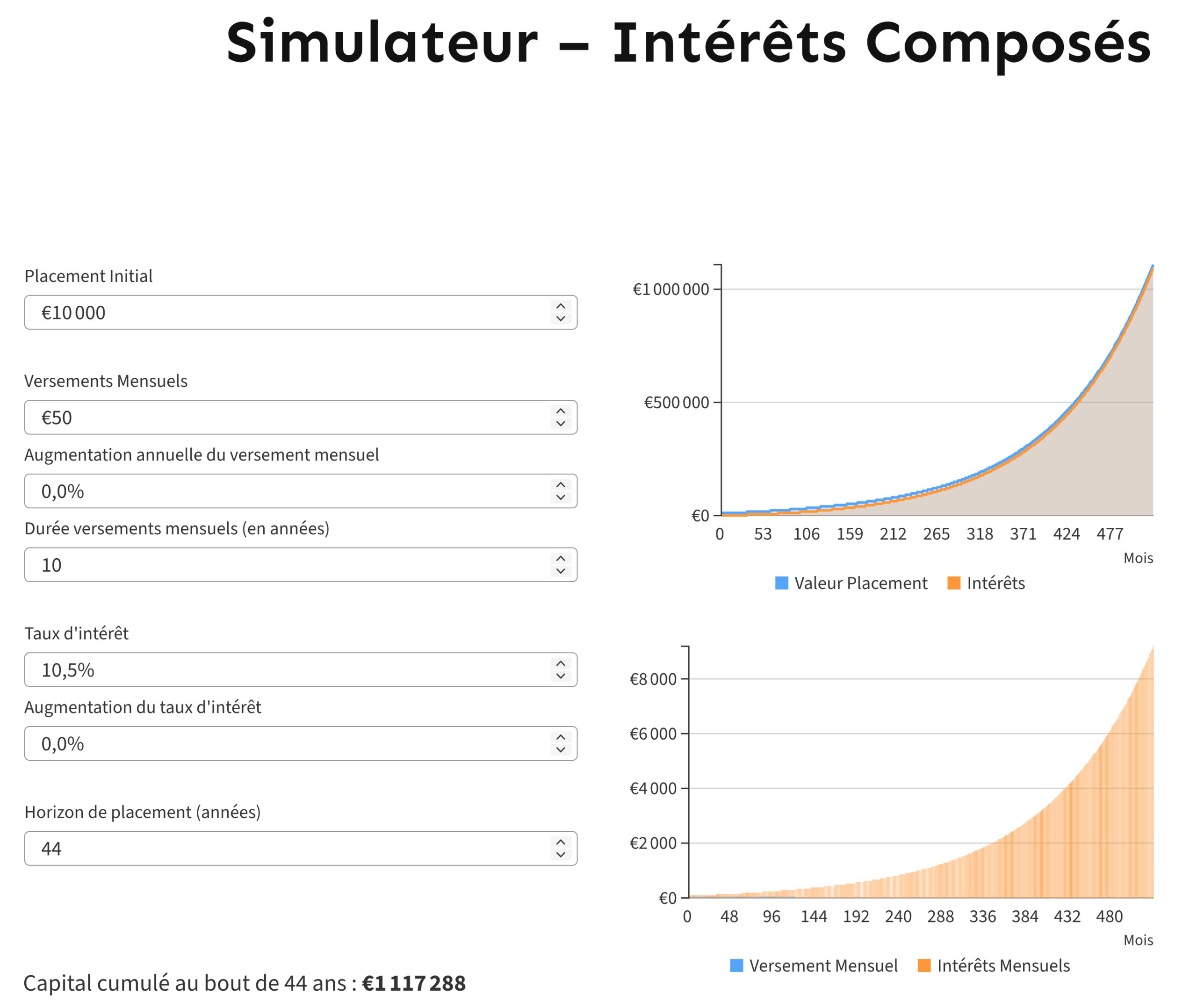
Bertrand : prendre son temps pour investir
Bertrand a au contraire pris son temps pour commencer à investir. Il a fait les mêmes études universitaires qu’Anne, qu’il a complété par un master qui lui a coûté 10 000 euros.
Il commence à travailler à l’âge de 27 ans. Mais il ne commencera à investir qu’à l’âge de 30 ans dans la même assurance-vie.
N’ayant pas encore de famille et n’ayant plus de prêt, il va investir initialement 20000 euros et versera 100 euros tous les mois jusqu’à la retraite. Bertrand n’arrêtera jamais ses versements.
Voici ce qu’il obtient :
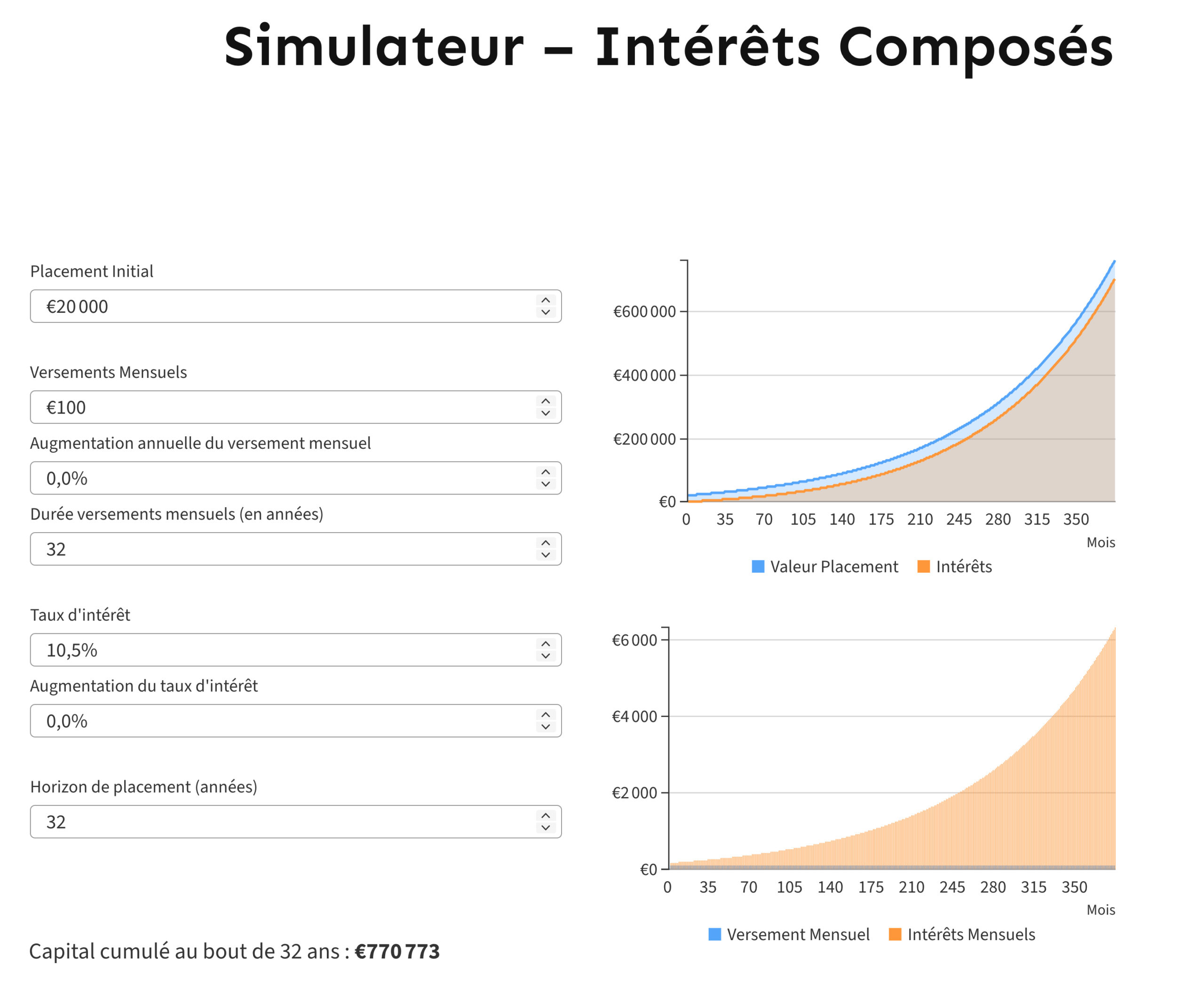
La puissance des intérêts composés se manifeste sur le long terme.
Même si vous investissez moins ou que vous arrêtiez en cours de route!
En effet, Anne a versé dans son assurance-vie beaucoup moins d'argent que Bertrand et beaucoup moins longtemps. Mais elle a réussi à se constituer un capital plus conséquent car elle avait commencé plus tôt.
Il faut commencer le plus tôt possible à investir pour tirer profit au maximum de l’effet multiplicateur des intérêts composés et atteindre l’indépendance financière plus rapidement.
Doubler son capital : la règle des 72
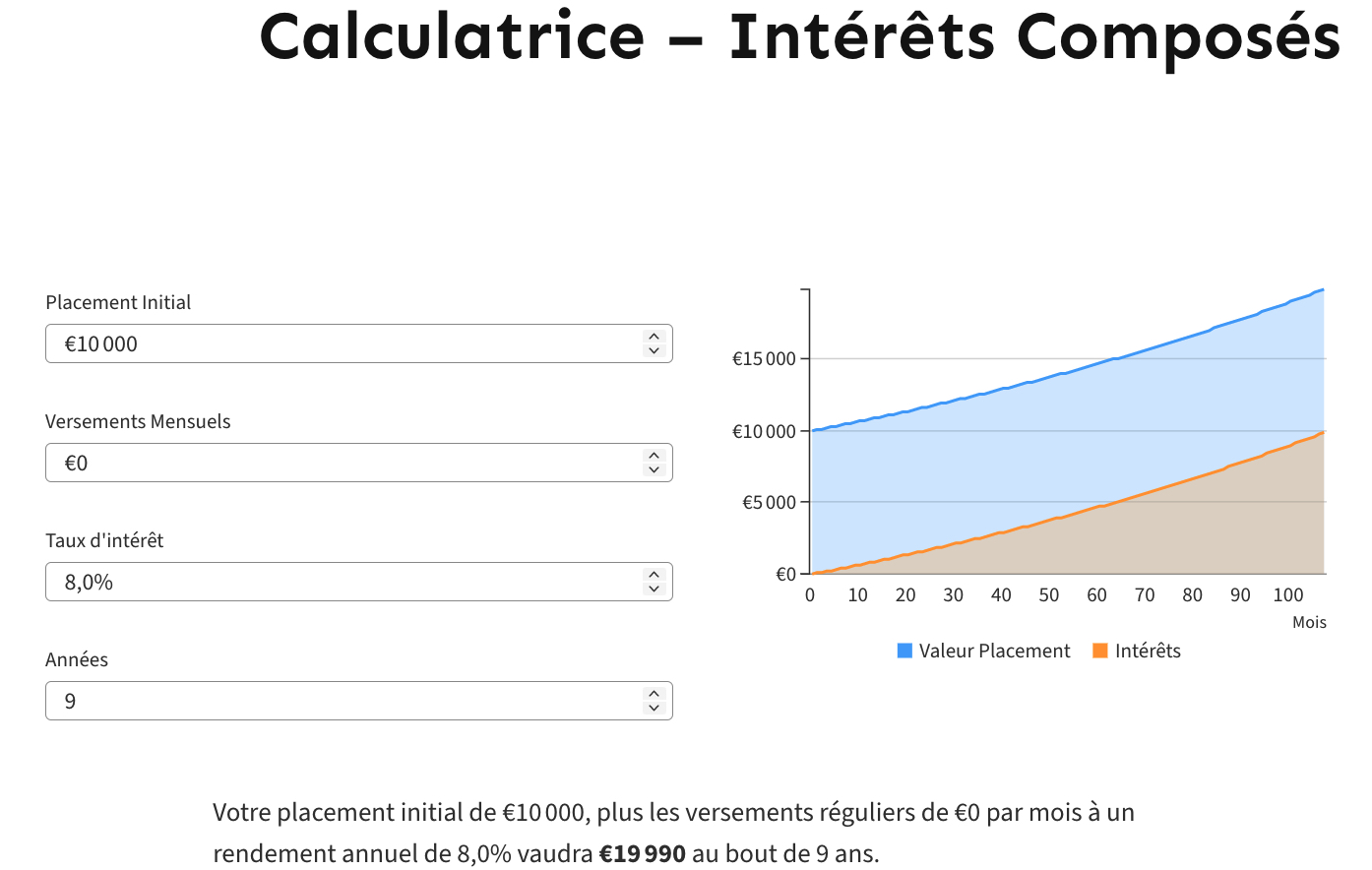
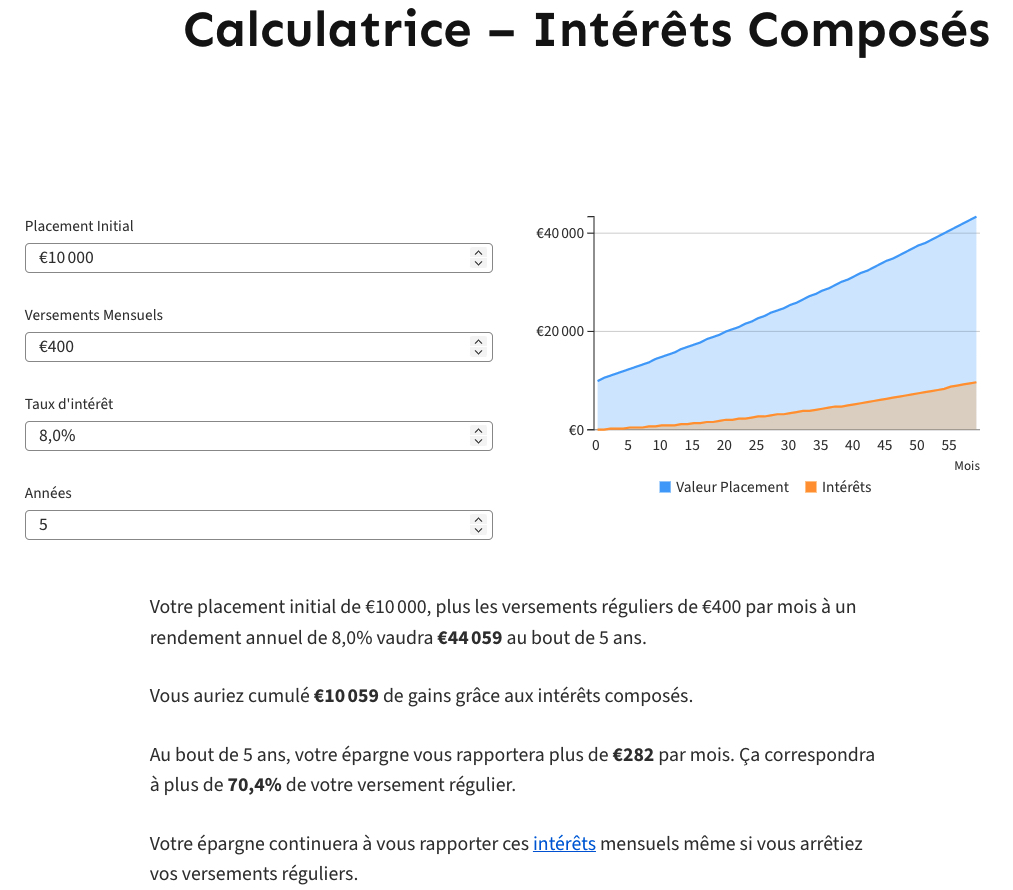
La règle des 72 est une méthode simple et rapide pour estimer le nombre d’années nécessaires pour doubler votre capital. Cette durée s’obtient en divisant 72 par le taux d’intérêt espéré. Ainsi un capital placé à 8% mettra 9 ans pour être doublé car 72 divisé par 8 donne 9.
Cette règle est approximative mais efficace. Elle est illustrée par ce calcul effectué à l’aide de la calculatrice d’intérêts composés du blog :
Tripler son capital : la règle des 120
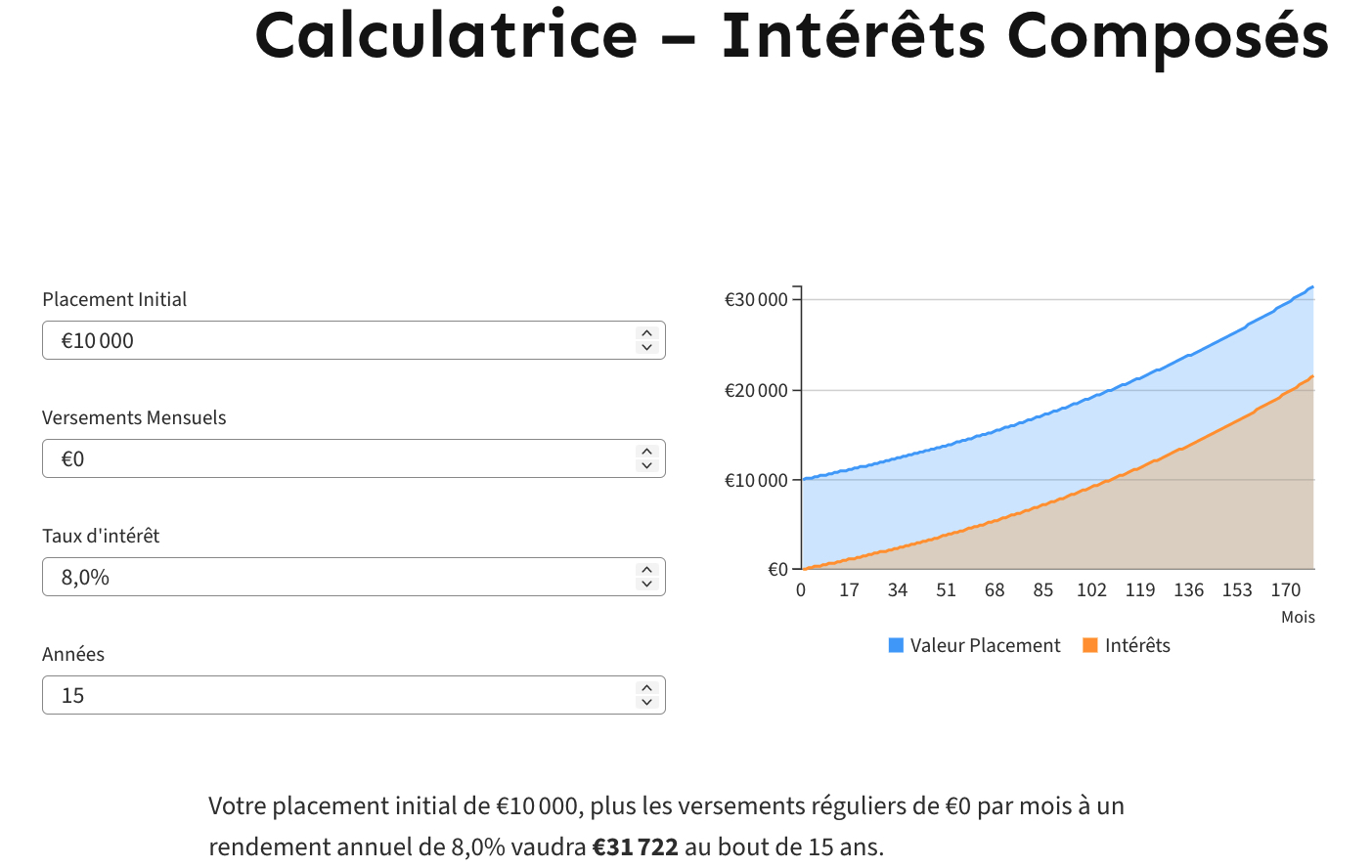
La règle des 120 est une méthode simple et rapide pour estimer le nombre d’années nécessaires pour tripler votre capital. Cette durée s’obtient en divisant 120 par le taux d’intérêt espéré. Ainsi un capital placé à 8% mettra 15 ans pour être doublé car 120 divisé par 8 donne 15.
Comme la règle des 72, la règle des 120 est approximative mais efficace. Elle est illustrée par ce calcul effectué à l’aide de la calculatrice d’intérêts composés disponible dans la section Outils du blog :
Comment devenir rentier avec les intérêts composés
Le secret pour devenir rentier réside probablement dans cette parole de Warren Buffett : « Si vous ne trouvez pas un moyen pour faire de l’argent pendant que vous dormez, vous travaillerez jusqu’à votre mort ».
Le lien avec l’intérêt composé ?
Les intérêts composés travaillent pour vous pendant que vous dormez, pendant que vous travaillez, tout le temps, 24h/24 et 365 jours par an.
Mais il y a un moment précis où les intérêts composés vont vous rapporter plus que votre effort d’épargne.
Même sans apport initial.
Et ça ne prend pas 40 ans pour y arriver.
Vous y arriverez d’ailleurs relativement rapidement.
Le simulateur que j’ai développé permet d’identifier ce moment.
Illustration
Regardons l’exemple suivant : vous prenez un investissement qui rapporte 7% par an (c’est à peu près en ligne avec le CAC40 dividendes réinvestis) et vous versez 500 euros chaque mois dans ce placement avec un apport initial de 0 euro.
Voici ce que donne le simulateur d’intérêts composés pour ce placement :
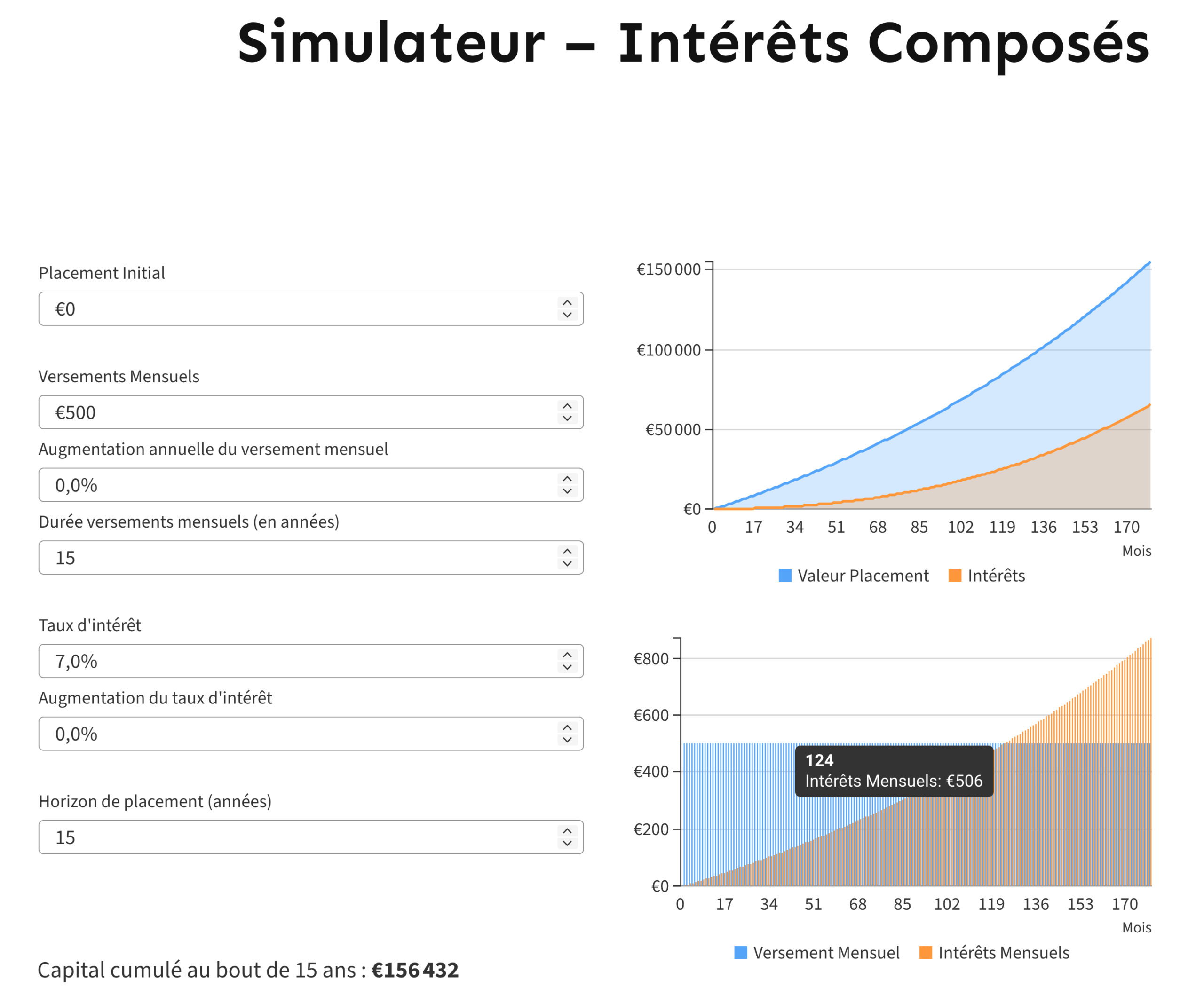
Au bout de 124 mois (10 ans et 4 mois) vous obtiendrez 506 euros par mois en intérêts mensuels (il s'agit bien sûr d'une moyenne qui peut fluctuer en fonction de la volatilité des marchés).
En d’autres termes, en moins de 11 ans votre placement vous rapportera plus ce que vous investissez de votre poche. Vous pourrez d’ailleurs arrêter d’épargner tous les mois. Votre placement continuera à vous rapporter de plus en plus chaque mois :
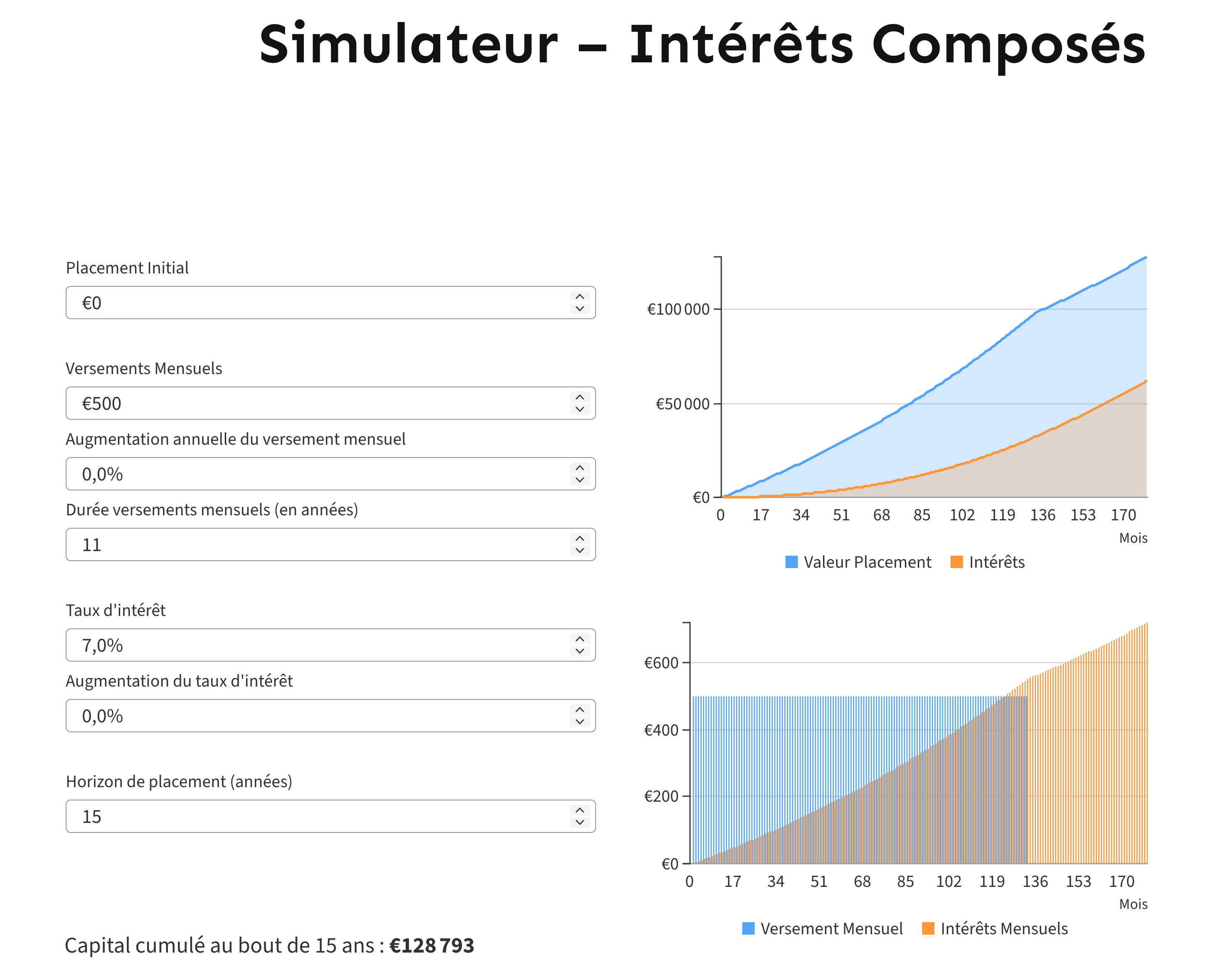
Si vous investissez suffisamment et régulièrement les intérêts composés vous permettront d’avoir un revenu complémentaire, voire de de devenir rentier. Il est là le secret de la richesse et de la liberté financière.
C’est aussi la principale raison pour laquelle les riches sont de plus en plus riche. Leur argent est investi et continue à rapporter tous les mois beaucoup plus que ce qu’ils ont placé eux-mêmes.
C'est comme ça qu'ils deviennent rentiers sur des générations.
La bonne nouvelle c’est que c’est accessible à tout le monde.
Quiz : investissement, intérêts composés et liberté financière
J’ai créé pour cela un quiz qui vous permet de faire le point sur vos investissements et votre approche de vos finances.
A la fin du quiz vous aurez accès à une analyse des réponses que vous obtiendrez gratuitement par email et qui vous permettra de découvrir les stratégies qui permettent de profiter au maximum de la puissance des intérêts composés pour atteindre votre indépendance financière.
Pour y accéder il vous suffit de cliquer sur le bouton !
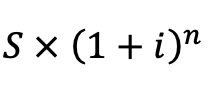
Bonjour
Est il possible d’avoir un simulateur en xls ?
Merci !
Bonjour,
Merci pour votre commentaire.
Tous les simulateurs et calculateurs sont accessibles gratuitement et en illimité dans la section « Calculateurs Financiers » du site.
N’hésitez pas à les utiliser.
Radhi